Relationship between internal volume and leak
Equivalent Internal Volume
The amount of differential pressure change due to leak depends on the internal volume of the entire measurement system, including the work and tester. It is also closely related to the measurement time.
The Air Leak Tester uses a coefficient called Equivalent Internal Volume (Ve), which takes into account the effect of pressure fluctuation factors (volume change due to internal pressure of the work and differential pressure sensor) in the entire measurement system.
The Equivalent Internal Volume can be calculated using the following equations.
Depending on the model of the Air Leak Tester, the Ve value can be measured directly using the Auto Leak Calibrator (ALC) or Leak Master.
-
Ve = Vw + Vt + {Ks(1 + Vw / Vm) + Kw}(101.3 + P)Under the conditions above:
Vw = Vm (Work and master have the same volume)
Ks = 0.01 mL / kPa or 0.005 mL / kPa (Depends on the model)
Kw = 0 mL / kPa (No change in work volume)
Ks(1 + Vw / Vm) + Kw = 2 Ks - When Ks = 0.01 mL / kPa
Ve = Vw + Vt + 0.02(101.3 + P) - When Ks = 0.005 mL/kPa
Ve = Vw + Vt + 0.01(101.3+P)
Ve: Equivalent Internal Volume (mL)
Vw: Internal volume of work and piping (mL)
Vt: Internal volume of tester (mL) Vt = 9 mL
Ks: Sensor volume change relative to pressure (mL/kPa)
Kw: Work volume change relative to pressure
P: Test pressure (kPa)
Leak Rate
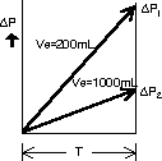
Relations between Equivalent Internal Volume and leak Q
Q: Leak (mL/min) ΔP: Differential pressure (Pa) Ve: Equivalent Internal Volume (mL) T: Detection time (s)
- Example: A differential pressure of 16 Pa is generated during a Detection of 3 seconds when the Equivalent Internal Volume is 800 mL.
What is the leak in this case?
【Note】
The differential pressure generated by leak is inversely proportional to the Equivalent Internal Volume.
- Example: If the ratio of Equivalent Internal Volume is 1:5, the differential pressure for the same leak will be 5:1.
Q: 5 mL / min
T: 2 s
When Ve = 200 mL, ΔP1 = 85 Pa
When Ve = 1000 mL, ΔP2 = 17 Pa
Reference: Gas Pressure and Properties
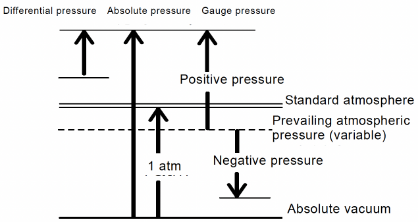
A. Absolute pressure: Pressure based on absolute vacuum
Example: PaA, kg / cm 2A (or kg/cm2abs), Torr (absolute pressure = atmospheric pressure + gauge pressure)
B. Gauge pressure: Pressure based on atmospheric pressure
(pressure/vacuum) Example: PaG, kg / cm2G/
C. Differential pressure: The difference between two pressures. Example: PaD、kg / cm2D

Pressure Units
1 bar = 0.1 MPa = 1.01972 kg / cm2, 1 Pa = 1 N / m2, 1 Torr = 1 mmHg
Scroll
| Pa | kg / cm2 | mmH2O | mmHg | PSI | |
|---|---|---|---|---|---|
| 1Pa | 1 | 1.01972 × 10 E-5 | 0.101972 | 7.50062 × 10 E-3 | 1.45038 × 10 E-4 |
| 1kg/cm2 | 9.80665 × 10 E4 | 1 | 10 E4 | 735.559 | 14.2233 |
| 1mmH2O | 9.80665 | 10 E-4 | 1 | 7.35559 × 10 E-2 | 1.42233 × 10E-3 |
| 1mmHg | 133.322 | 1.35951 × 10 E-3 | 13.5951 | 1 | 1.93368 × 10 E-2 |
| 1PSI | 6894.76 | 7.03070 × 10 E-2 | 703.070 | 51.7149 | 1 |
※10E-3stands for 10 to the power of -3
Ideal Gas Law
There is a fixed relationship among the three quantities of pressure, volume, and temperature of gas, and once two of these quantities are determined, the remaining one is inevitably determined. The equation that expresses the relationship between these three quantities is called the state equation, which is based on the “Combined Gas Law”.
(1) PV=GRT
Initial state, Final state
When (V1,P1,T1) → (V2,P2,T2)
(2) If the temperature is constant T1 = T2, P1・V1 = P2・V2
(3) If the volume is constant V1 = V2, P1 / T1 = P2 / T2
P: Absolute pressure
V: Volume
G: Gas weight
T: Absolute temperature
R: Gas constant